I am the lead coder for the re-development of Bertini from C into C++ with Python. The project is going along nicely, and is graciously supported by the NSF.

Bertini is a program for solving polynomial systems, involving many functions in many variables. Categorically, it is a tool in Numerical Algebraic Geometry, although scientists and engineers from outside this area of applied mathematics successfully use it for solving a variety of problems, including stationary points of differential equations, kinematic mechanism design, solving PDE's, and others.

An old adage of mathematics is,

when you can't solve a problem, solve a different problem.

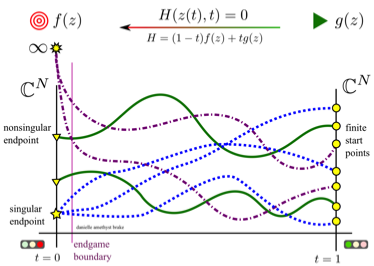
In this case, you want to solve a polynomial system \(f(x)\) . But it's hard. Too hard. Impossible. So instead, you solve \(g\), a different but related system. You can spend anywhere from almost no time, to a long time, finding and solving \(g\). This is the start system.

Then, you deform from \(g\) to \(f\) through some path variable or time variable, \(t\). You track the homotopy path, using predictor-corrector methods, using an endgame near the target \(t\) value. In Bertini, we track from \(t = 1\) to \(t = 0\).

This is summarized in the below diagram. If you use it in something, please credit me. If you want the full-res non-blurry version, email me, and I will send you a better version!

Currently the program can:

• parse arbitrary systems into our new hybrid double and multiple-precision evaluation tree set of classes,
• evaluate in double or multiple-precision at any number of digits
• differentiate, to produce a single evaluation tree for the Jacobian of a system
• evaluate the Jacobian in any precision,
• form the Total Degree start system for an arbitrary polynomial system, and generate its solutions without pre-storage
• form the MultiHomogeneous start system
• couple a path variable between any two systems, to form a final homotopy for evaluation during tracking.
• do path tracking in double, fixed, and adaptive multiple precision
• run the fractional power series and cauchy endgames
• solve generic systems of polynomials
• do all of the above in Python via the provided bindings in PyBertini

We have flow charts for implementation of path tracking, with Euler prediction and Newton correction.

Next steps will be:

• creation of a class or method for passing around configurations for various algorithms
• implementation of MPI methods for parallelizing the program -- homotopy continuation is `pleasantly parallel'.
• continued development of tests

The program uses these excellent libraries, among others:

• Boost.Multiprecision -- and hence MPFR and GMP
• Boost.Spirit.Qi and Karma
• Eigen 3

I have collaborated on this project with no fewer than

• Jon Hauenstein, my former postdoc mentor at Notre Dame
• Dan Bates, my former postdoc mentor at Colorado State
• Jeb Collins, a friend at University of Mary Washington
• Tim Hodges
• Alan Liddell

and receive additional advisorship from

• Andrew Sommese
• Charles Wampler

and further collaboration with

• Hythem Sidky
• Matthew Niemerg
• Francesco Pancaldi

Bertini2 is hosted on Github, and is under the GPL V3 license for FOSS. Do you want to help? Send me an email! Fork the repo! File an issue or submit a pull request!

Paramotopy is a parallel parametrized polynomial system solver, written by myself, Matt Neimerg, and Dan Bates. It is implemented in C++ and linked against Bertini, and embracing the power of the Boost suite of libraries, with MPICH for parallelism. Paramotopy uses a numeric text menu driven interface, and features failed path resolution, mesh and user-supplied sampling methods, anomaly searching, and persistent settings.

Bertini_real is a numerical decomposer for algebraic surfaces and curves. From polynomials in a text input file, the program ultimately will provide you with a STL file you can supply to a thickening program and 3D print. It is written in C++, using Bertini, MPICH, and Boost. Its interface is through the command line, and a Matlab suite is provided for processing the plain text output into something useable by a human.

We have three papers on the topic -- two extended abstracts summarizing the theoretical advancements (one on the implementation, and another on the decomposition of surfaces including singular curves), and one submitted paper on the software itself.

My coauthors for the project at Dan Bates, Wenrui Hao, Jon Hauenstein, Andrew Sommese, and Charles Wampler.

The project homepage is at bertinireal.com, and you can find sourcecode at github.com

My 3d printed surfaces in my galleries have almost all been generated from Bertini_real.

Bertini_tropical is Matlab code wrapping around Bertini, for numerically computing real and complex tropical curves in any number of dimensions.

This project is joint work with Cynthia Vinzant and Jon Hauenstein.

There is one submitted paper, available on the Arxiv.