Tuelle

Equation
\[ yz(x^2+y-z) \]
Properties:
- degree 4
- unbounded
- reducible, two components of degree 1, and one component of degree 2


Some story
I found Tuelle to be a most instructive surface. Prior to decomposing it, I believed that one could ignore components by virtue of witness sets. Just use the witness points for the component you are interested in. I was wrong. While this allows you to work on the one component, you miss intersections of components whose witness sets you ignored. That is, if your components intersect, to have a complete picture, you need all witness sets.
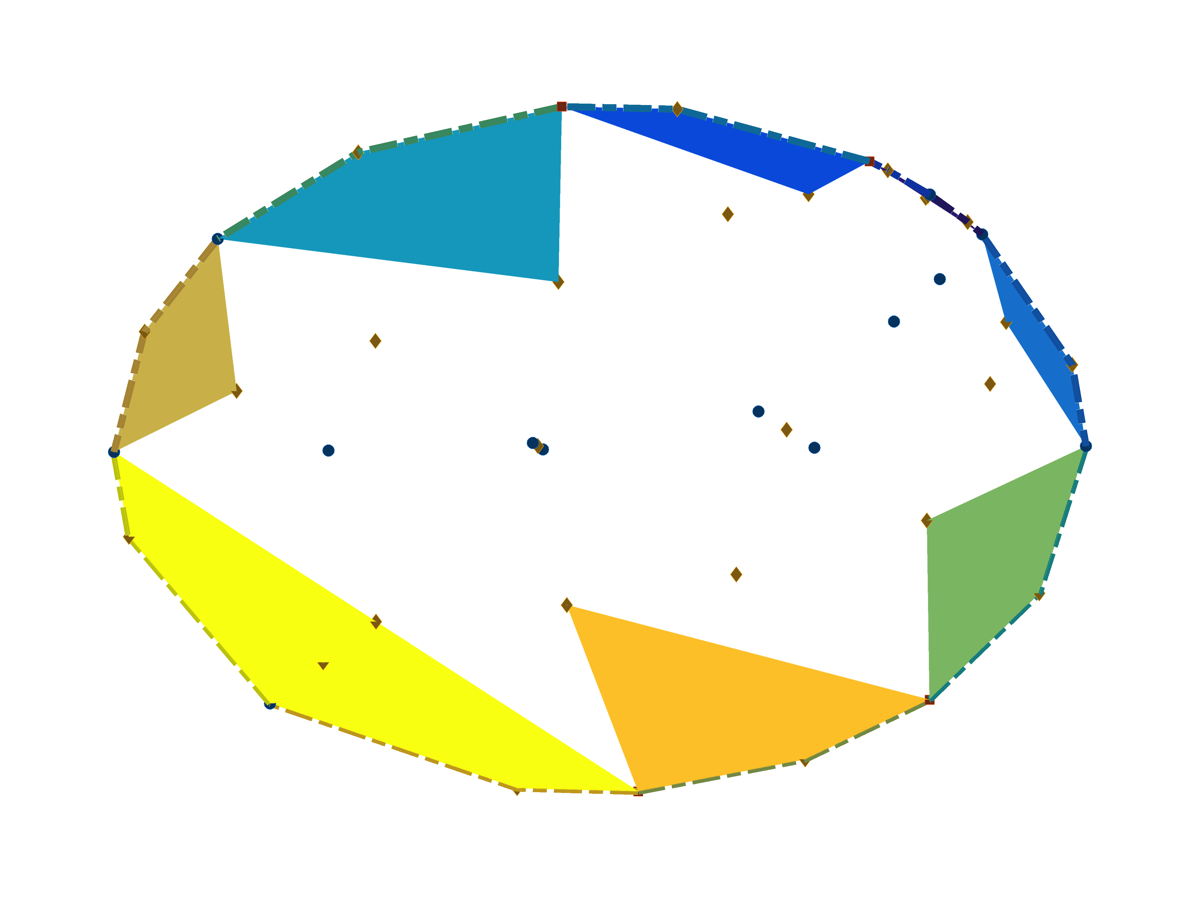
In the below picture, I show a single degree-1 component (ok, a plane) of this variety. I used just the single witness point for this component to do the decomposition. Note the blue dots, which occur on the critical curve -- or do they? Yes, they do, but since the critical curve includes curves of intersection as singular curves, and I didn't use witness points for those components, we miss these parts of the critical curve. Hence, the surface has holes around these points. Only by either using all witness points for all components, or by re-phrasing the system, can we get the complete picture.
input